|
clipper
|
|
clipper
|
Represents a polynomial in the Bernstein-Bezier basis using Bezier coefficients. More...
Public Member Functions | |
| PolynomialBezier (const std::vector< Numeric > &coefficient) | |
| unsigned int | degree () const |
| Return degree of the polynomial. | |
| Numeric | coefficient (unsigned int i) const |
| Return a Bezier coefficient. | |
| std::string | toString (const std::string &T="") const |
| Return polynomial as latex math string. | |
| std::string | toPolygon () const |
| Return Bezier coefficients as a polygon. | |
| std::vector< std::pair < Numeric, Numeric > > | getConvexHull () const |
| Return the convex hull of the Bezier coefficients calculated using Jarvis's march. | |
| std::vector< Numeric > | getConvexHullIntersection () const |
| Return the convex hull of the Bezier coefficients calculated using Jarvis's march. | |
| std::string | toConvexHullString () const |
| Return the convex hull of the Bezier coefficients for plotting. | |
| class PolynomialStandard< Numeric > | toStandard () const |
| Transform the polynomial from Bernstein-Bezier basis back to the standard monomial basis. | |
| Numeric | evaluate (Numeric X) const |
| Calculate the polynomial's value at the position X using the schema of de Casteljau. | |
| std::pair< PolynomialBezier, PolynomialBezier > | deCasteljauSplit (Numeric t0) const |
| Similar to evaluate: run de Casteljau's algorithm and output the Bezier coefficients of interval [0,t0] and [t0,1] as separate polynomial objects. | |
| std::vector< Numeric > | findRoots () const |
| Calculate all real roots for a quadratic or cubic polynomial in Bezier representation (according to Remark 3 in [1]). | |
| PolynomialBezier | interpolateDegree (int k) const |
| This function is the heart of the root finding algorithm: reduce or raise the degree of this polynomial to k. | |
| PolynomialBezier | interpolateDegree (const class Matrix< Numeric > &m) const |
| This function is the heart of the root finding algorithm: reduce or raise the degree of this polynomial by applying a matrix. | |
| Numeric | maxCoefficientDeltaTo (const PolynomialBezier &b) const |
| Compare two Bezier polynomials of same degree and return the maximum difference between pairs of coefficients. | |
| PolynomialBezier | operator+ (const Numeric &v) const |
| Create a new polynomial shifted upwards by adding v to all coefficients. | |
| PolynomialBezier | operator- (const Numeric &v) const |
| Create a new polynomial shifted downwards by subtracting v from all coefficients. | |
Private Attributes | |
| std::vector< Numeric > | m_coefficient |
The n+1 Bezier coefficients to the Bernstein polynomials basis ( 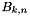 ) ) | |
Represents a polynomial in the Bernstein-Bezier basis using Bezier coefficients.
Definition at line 1061 of file clipper.cc.
| PolynomialBezier< Numeric >::PolynomialBezier | ( | const std::vector< Numeric > & | coefficient | ) | [inline, explicit] |
Definition at line 1072 of file clipper.cc.
| Numeric PolynomialBezier< Numeric >::coefficient | ( | unsigned int | i | ) | const [inline] |
Return a Bezier coefficient.
Definition at line 1084 of file clipper.cc.
| std::pair<PolynomialBezier,PolynomialBezier> PolynomialBezier< Numeric >::deCasteljauSplit | ( | Numeric | t0 | ) | const [inline] |
Similar to evaluate: run de Casteljau's algorithm and output the Bezier coefficients of interval [0,t0] and [t0,1] as separate polynomial objects.
This is later used to branch when finding roots.
Definition at line 1300 of file clipper.cc.
| unsigned int PolynomialBezier< Numeric >::degree | ( | ) | const [inline] |
Return degree of the polynomial.
Definition at line 1078 of file clipper.cc.
| Numeric PolynomialBezier< Numeric >::evaluate | ( | Numeric | X | ) | const [inline] |
Calculate the polynomial's value at the position X using the schema of de Casteljau.
Definition at line 1277 of file clipper.cc.
| std::vector<Numeric> PolynomialBezier< Numeric >::findRoots | ( | ) | const [inline] |
Calculate all real roots for a quadratic or cubic polynomial in Bezier representation (according to Remark 3 in [1]).
Imaginary roots are ignored.
Instead of using the Cardano's formulas in Bezier form as in [2], we return to the monomial base case for calculating the roots
Definition at line 1331 of file clipper.cc.
| std::vector< std::pair<Numeric,Numeric> > PolynomialBezier< Numeric >::getConvexHull | ( | ) | const [inline] |
Return the convex hull of the Bezier coefficients calculated using Jarvis's march.
Definition at line 1126 of file clipper.cc.
| std::vector<Numeric> PolynomialBezier< Numeric >::getConvexHullIntersection | ( | ) | const [inline] |
Return the convex hull of the Bezier coefficients calculated using Jarvis's march.
Definition at line 1178 of file clipper.cc.
| PolynomialBezier< Numeric > PolynomialBezier< Numeric >::interpolateDegree | ( | int | k | ) | const |
This function is the heart of the root finding algorithm: reduce or raise the degree of this polynomial to k.
Apply a degree rasing of reducing matrix, where the matrix has to be constructed before application.
Definition at line 1651 of file clipper.cc.
| PolynomialBezier PolynomialBezier< Numeric >::interpolateDegree | ( | const class Matrix< Numeric > & | m | ) | const |
This function is the heart of the root finding algorithm: reduce or raise the degree of this polynomial by applying a matrix.
| Numeric PolynomialBezier< Numeric >::maxCoefficientDeltaTo | ( | const PolynomialBezier< Numeric > & | b | ) | const [inline] |
Compare two Bezier polynomials of same degree and return the maximum difference between pairs of coefficients.
Definition at line 1395 of file clipper.cc.
| PolynomialBezier PolynomialBezier< Numeric >::operator+ | ( | const Numeric & | v | ) | const [inline] |
Create a new polynomial shifted upwards by adding v to all coefficients.
Definition at line 1406 of file clipper.cc.
| PolynomialBezier PolynomialBezier< Numeric >::operator- | ( | const Numeric & | v | ) | const [inline] |
Create a new polynomial shifted downwards by subtracting v from all coefficients.
Definition at line 1416 of file clipper.cc.
| std::string PolynomialBezier< Numeric >::toConvexHullString | ( | ) | const [inline] |
Return the convex hull of the Bezier coefficients for plotting.
Definition at line 1258 of file clipper.cc.
| std::string PolynomialBezier< Numeric >::toPolygon | ( | ) | const [inline] |
Return Bezier coefficients as a polygon.
Definition at line 1112 of file clipper.cc.
| PolynomialStandard< Numeric > PolynomialBezier< Numeric >::toStandard | ( | ) | const |
Transform the polynomial from Bernstein-Bezier basis back to the standard monomial basis.
Definition at line 1451 of file clipper.cc.
| std::string PolynomialBezier< Numeric >::toString | ( | const std::string & | T = "" | ) | const [inline] |
Return polynomial as latex math string.
Definition at line 1091 of file clipper.cc.
std::vector<Numeric> PolynomialBezier< Numeric >::m_coefficient [private] |
The n+1 Bezier coefficients to the Bernstein polynomials basis ( 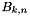 )
)
Definition at line 1067 of file clipper.cc.
 1.7.6.1
1.7.6.1