eSAIS - Inducing Suffix and LCP Arrays in External Memory
Posted on 2012-11-19 15:49 by Timo Bingmann at Permlink with 2 Comments. Tags: #research #stringology #stxxl #c++
This web page accompanies our conference paper "Inducing Suffix and LCP Arrays in External Memory", which we presented at the Workshop on Algorithm Engineering and Experiments (ALENEX 2013). A PDF of the publication is available from this site as alenex13esais.pdf or from the online proceedings. The paper was joint work with my colleagues Johannes Fischer and Vitaly Osipov.
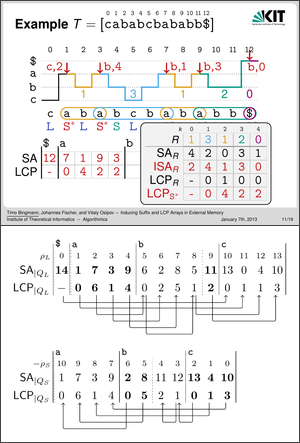
The slides to my presentation of the paper on January 7th, 2013 in New Orleans, LA, USA is available: alenex13esais-slides.pdf . They contain little text and an example of the eSAIS algorithm with a simplified PQ.
We have also submitted a full version of the eSAIS paper to a journal. Due to long publication cycles, we make a pre-print of the journal article is available here: esais-preprint.pdf . The full paper contains more details on the inducing algorithm for the LCP array and additional experimental details.
Our implementations of eSAIS, the eSAIS-LCP variants, DC3 and DC3-LCP algorithms as described in the paper are available below under the GNU General Public License v3 (GPL).
| eSAIS and DC3 with LCP version 0.5.4 (current) updated 2013-12-13 | ||
| Source code archive: (includes STXXL 1.4.0) | eSAIS-DC3-LCP-0.5.4.tar.bz2 | Browse online |
| Git repositories | Suffix and LCP construction algorithmsgit clone https://github.com/bingmann/eSAIScd eSAIS; git submodule init; git submodule update | |
STXXL 1.4.0git clone https://github.com/stxxl/stxxl | ||
For more information about compiling and testing the implementation, please refer to the README included in the source.