Finding Roots of Polynomials by Clipping - Report and Implementation from my Lab Course in Numerical Mathematics
Posted on 2012-03-20 22:29 by Timo Bingmann at Permlink with 0 Comments. Tags: #maths #university #c++
This semester I had the pleasure to take part in a lab exercise course supervised by Prof. Thomas Linß at the FernUniversity of Hagen. The objective was to comprehend, implement and evaluate a particular recent advancement in the field of numerical mathematics. My topic was finding the roots of a polynomial by clipping in Bézier representation using two new methods, one devised by Michael Bartoň and Bert Jüttler [1], the other extended from the first by Ligang Liu, Lei Zhang, Binbin Lin and Guojin Wang [2].
My implementation of this topic was done for the lab course in C++ and contains many in themselves interesting sub-algorithms, which are combined into the clipping algorithms for finding roots. These sub-algorithms may prove useful for other purposes, which is the main reason for publishing this website. Among these are:
- Polynomial classes for monomial and Bézier representations: PolynomialStandard and PolynomialBezier.
- Algorithms to convert from monomial to Bézier representation and vice versa: PolynomialStandard::toBezier() and PolynomialBezier::toStandard().
- Evaluation algorithms for both representations: Horner's Schema and the Algorithm of de Casteljau.
- Another version of de Casteljau's Algorithm to split a polynomial in Bézier representation into two parts.
- Jarvis' March aka gift wrapping (run time O(hn)) to calculate the convex hull of the Bézier polygon: PolynomialBezier::getConvexHull().
- Cardano's formulas to find all real roots of any cubic polynomial: PolynomialStandard::findRoots().
For the lab course I wrote two documents, both in German: one is an abstract Kurzfassung.pdf (1 page), which is translated into English below, and the other a short report Ausarbeitung.pdf
(6 pages). The report contains a short description of the algorithms together with execution and convergence speed measurements, which verify the original authors experiments. For presenting the lab work I created these Slides.pdf
, which however are not self-explanatory due to my minimum-text presentation style.
The implementation is a single file C++ program, which can optionally output LaTeX code for debugging purposes. The code can easily be compiled on any Linux machine, and probably also using other tool chains. It requires the GNU mpfr library for arbitrary precision floating-point numbers to enable high precision calculations (this library is also available for Visual C++). You can download the clipper.zip and view the corresponding doxygen HTML documentation.
The program can output LaTeX code documenting each individual steps of the computation while it is running, this method yields extremely detailed execution protocols for each input. For demonstration purposes the code contains nine different sets of examples, called demo1 through demo9. Among these demos six, seven and eight are speed test demos, which can be run without debugging overhead to measure the algorithms' run time. Results of these speed tests are documented in the short report above. The detailed execution protocols of the eight demos can downloaded below:
- demo1.pdf
(345 KiB) - Simple demonstration using a polynomial of 5th degree
- demo2.pdf
(561 KiB) - Polynomial of 8th degree with many roots in [0,1]
- demo3.pdf
(2.70 MiB) - Wilkinson polynomial with n = 20
- demo4.pdf
(269 KiB) - Unspecified demo to test other polynomials
- demo5.pdf
(228 KiB) - All degree reduction and raising matrices for degree five
- demo6.pdf
(6.36 MiB) - Speed test of polynomials with one single root
- demo7.pdf
(70.9 MiB) - Speed test of polynomials with a triple root (Warning: very large PDF)
- demo8.pdf
(5.29 MiB) - Speed test of polynomials with two near single roots
Abstract (Translation of Kurzfassung)
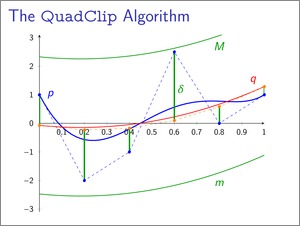
Fast computation of the roots of a polynomial is the basis for many more complex applications. Classical algorithms for this problem are for example bisection and the Newton-Raphson method, where the latter is quadratically convergent on single roots, but only linear convergent on double roots. In 2007, Bartoň und Jüttler [1] presented a new method, which is based on degree reduction and can find all roots of a polynomial within a given search interval. Like other numerical algorithms it is based on nested intervals enclosing the root and the new method exhibits a convergent rate of 3 for single roots and 3/2 for double roots. The method's scheme was continued in 2009 by Liu et al. [2] and their enhanced algorithm features convergent rate 4 for single roots, 2 for double roots and 4/3 for triple roots.
Both methods are based on approximating a polynomial of degree n given in Bernstein-Bézier representation by two polynomials of second or third degree, which bound the original polynomial from above and below. The roots of the polynomials of smaller degree can be found directly using the quadratic or Cardano's formulas and these roots yield smaller intervals which are recursively searched. The algorithms are iterated until a desired precision is reached and by branching into disjoint search internals, all roots of the polynomial can be found.
The convergent rates of the sequence of nested intervals is guaranteed by selecting the best-possible approximating polynomials of second or third degree. These can be calculated efficiently using a method developed by Jüttler, which is based on an explicit formula for the dual basis of the Bernstein polynomials. This method allows direct calculation of quadratic or cubic polynomials with smallest error distance to the target polynomial regarding the ![]() norm. In the end, the degree reduction operation is a simple matrix multiplication.
norm. In the end, the degree reduction operation is a simple matrix multiplication.
[1] Bartoň, M. and Jüttler, B. "Computing roots of polynomials by quadratic clipping", Computer Aided Geometric Design 24.3, (2007) p. 125-141. DOI: 10.1016/j.cagd.2007.01.003
[2] Liu, L., Zhang, L., Lin, B., Wang, G. "Fast approach for computing roots of polynomials using cubic clipping", Computer Aided Geometric Design 26.5, (2009), p. 524-599. DOI: 10.1016/j.cagd.2009.02.003